Let's build GameplayKit - Pathfinding
04 Jul 2015Now we’re getting to the fun stuff. GameplayKit provides 3 ways to do pathfinding:
- On a 2D grid, like in a tactical RPG or checkers or something.
- On a graph in a 2D plane with obstacles in the way.
- On an arbitrary directed graph.
I’m going to start with the third one there, because GameplayKit treats it as the base that the other two are built upon.
The core building block in GameplayKit’s pathfinding implementation is GKGraphNode. In fact , at least for the arbitrary directed graph case GKGraphNode is all you need. GKGraph just serves as a handy place to hold your nodes.
Let’s take a quick look at the GKGraphNode interface:
@interface GKGraphNode : NSObject
@property (readonly, nonatomic) NSArray *connectedNodes;
- (void)addConnectionsToNodes:(NSArray *)nodes bidirectional:(BOOL)bidirectional;
- (void)removeConnectionsToNodes:(NSArray *)nodes bidirectional:(BOOL)bidirectional;
- (float)costToNode:(GKGraphNode *)node;
- (float)estimatedCostToNode:(GKGraphNode *)node;
- (NSArray *)findPathToNode:(GKGraphNode *)goalNode;
- (NSArray *)findPathFromNode:(GKGraphNode *)startNode;
@endNo reference to GKGraph in there. The -add/removeConnections methods set up direct links from the target node to the nodes in the array: the graph is directed, so if you want your characters to be able to move in either direction, set bidirectional to YES.
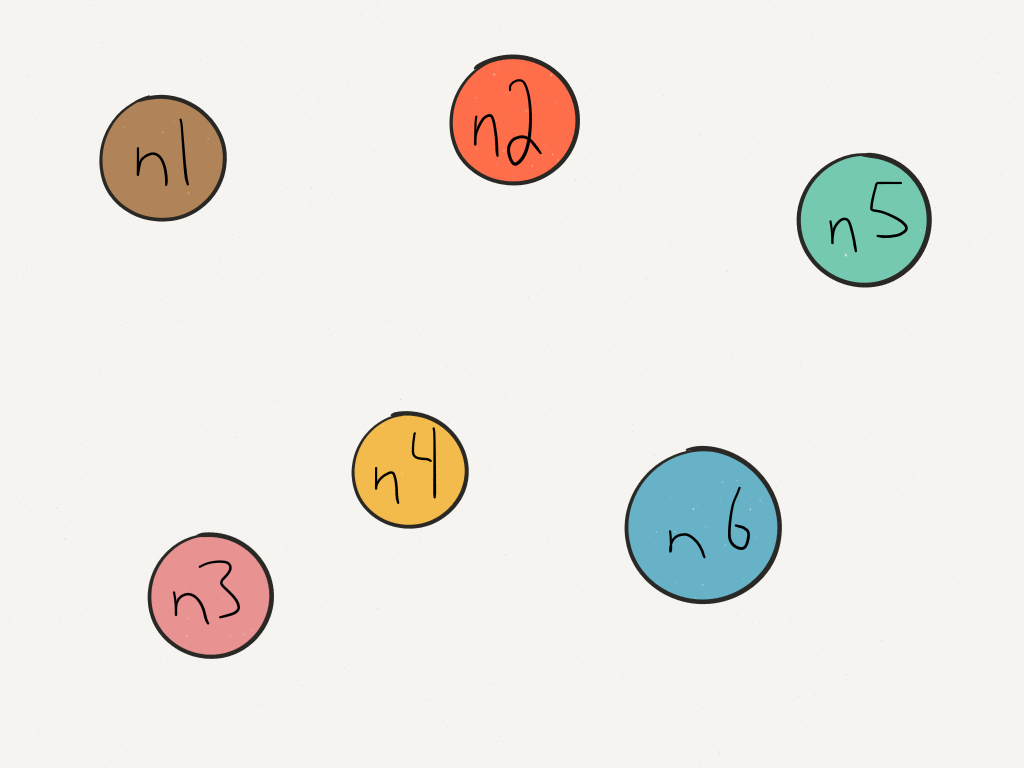
So given this set of nodes:
Running this:
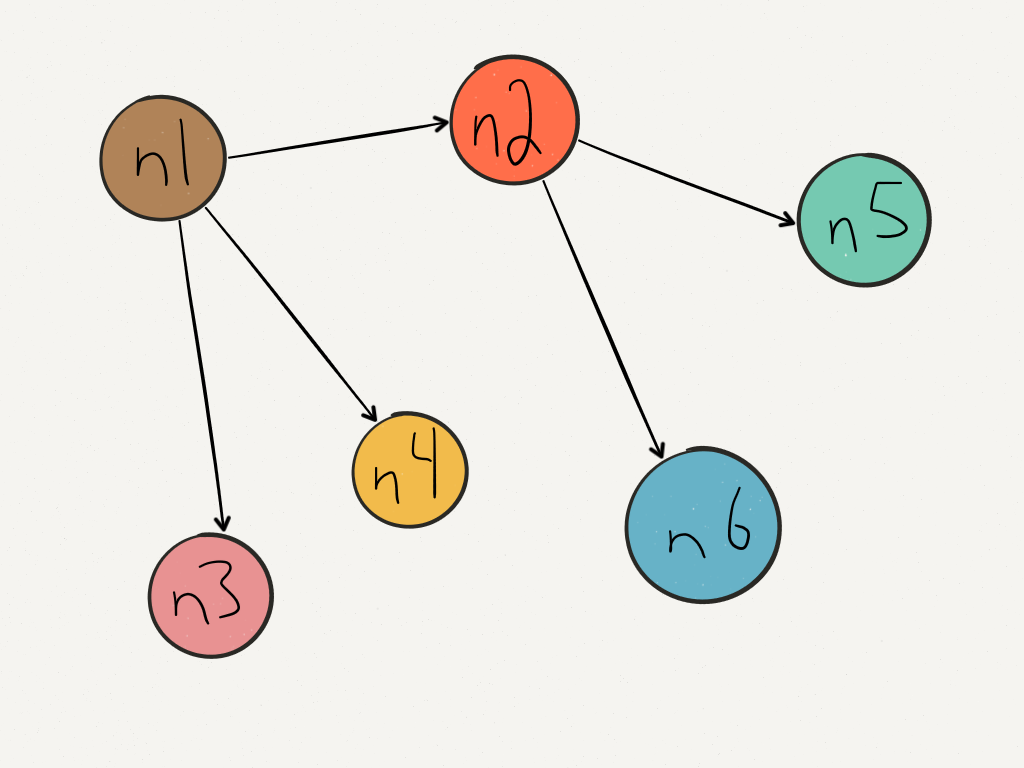
[n1 addConnectionsToNodes:@[n2, n3, n4] bidirectional:NO];
[n2 addConnectionsToNodes:@[n5, n6] bidirectional:NO];Will end up with the graph connected like this:
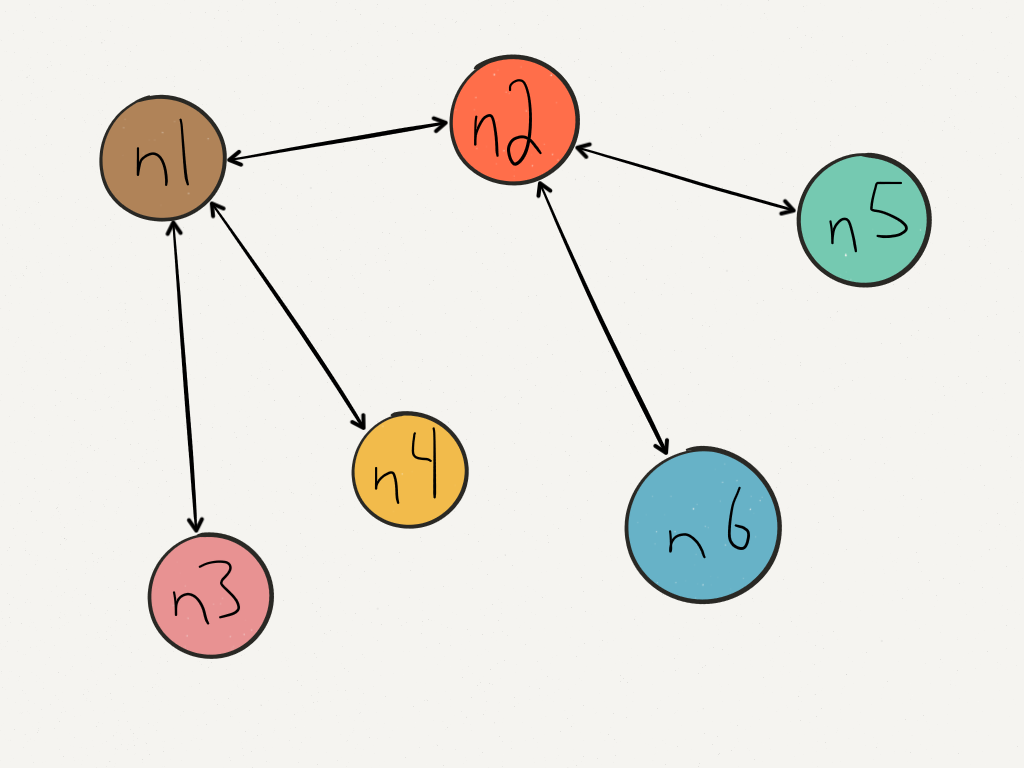
If instead we set bidirectional to YES, we’ll get this:
The code’s straightforward (I left input validation out here for brevity):
- (void)addConnectionsToNodes:(NSArray *)nodes bidirectional:(BOOL)bidirectional
{
for (GKGraphNode *node in nodes) {
[self.nodes addObject:node];
if (bidirectional) {
[node addConnectionsToNodes:@[self] bidirectional:NO];
}
}
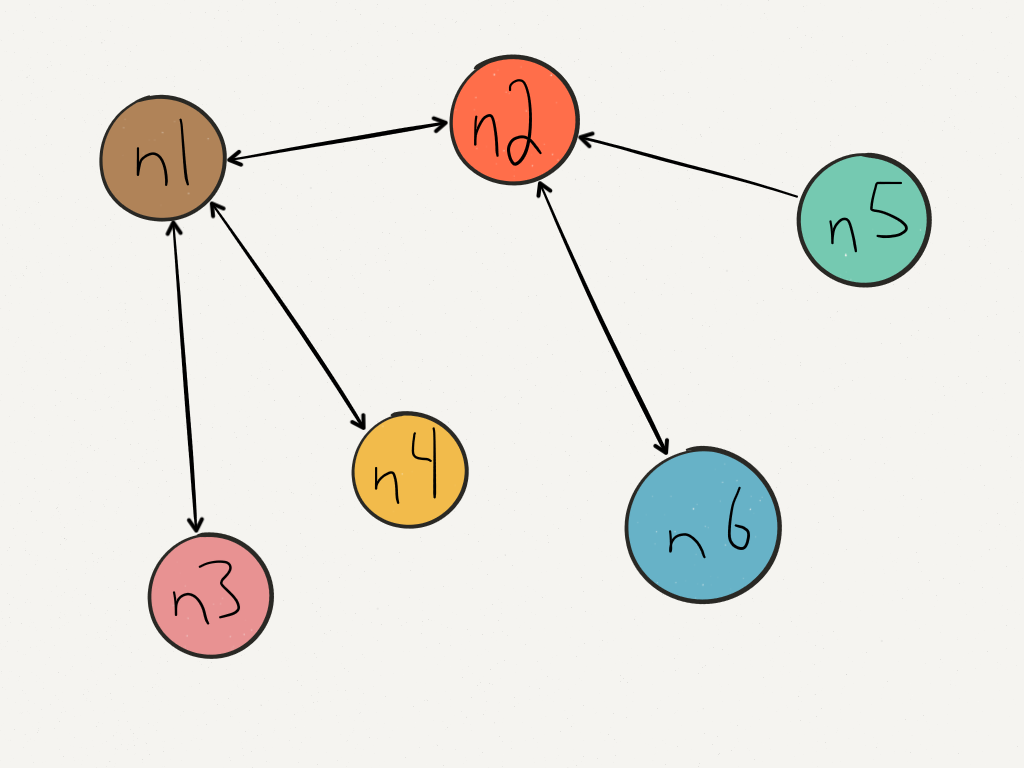
}-removeConnections works the same way. Given the graph in that last image, [n2 removeConnectionsToNodes:@[n5] bidirectional:NO] would result in this graph:
The connection from n2 to n5 is gone, but the connection from n5 to n2 is still there. The code for this looks pretty much the same as for addConnections.
(As I draw all this up I now have a nice set of test cases to add to the code. 👍)
-costToNode: returns a floating point value that signifies how expensive it is to move from one node to another. The base GKGraphNode implementation returns 1 for any node that is in that node’s direct connection list, for example, [n1 costToNode:n4] will return 1. It’s not specified what value is returned if you call -costToNode: with a node that there’s no connection to: I’m opting to return FLT_MAX in that case.
-estimatedCostToNode: is a heuristic value, or guess. To get in to what that means we need to think about what algorithm is going to be backing the pathfinder. My guess is A*: it’s well known, very common in games, performant, and perhaps most important, it’s general enough to work for all 3 types of pathfinding GameplayKit offers.
The best place I know of to learn more about A* is Amit’s A* Pages. If you take a look at his introduction you’ll see Dijkstra’s Algorithm and Best-First-Search mentioned, and if you read a bit further into the heuristics page there’s an important fact mentioned in the first bullet point:
At one extreme, if h(n) is 0, then only g(n) plays a role, and A* turns into Dijkstra’s algorithm, which is guaranteed to find a shortest path.
Our base GKGraphNode isn’t defined on a grid, it’s just a collection of nodes with connections between them: there’s no spatial information in there at all. At a glance it seems like A* might not work, because there’s no useful heuristic we can give it. However, if we make the heuristic function return 0, A* turns into Dijkstra’s algorithm and it’ll work just fine.
So that’s what we do in the base implementation of GKGraphNode -estimatedCostToNode: always return 0. When we get to the other two implementations we’ll implement this in different ways.
Two methods left: -findPathToNode: and -findPathFromNode:. There are methods for going both ways because the graph isn’t always going to be bidirectional, so the path between two nodes isn’t necessarily going to be the same in both directions. The second one can be defined in terms of the first:
- (NSArray *)findPathFromNode:(GKGraphNode *)startNode
{
return [startNode findPathToNode:self];
}
That just leaves us implementing A*! I’ve done this before, but it was a much less general implementation, so this’ll be neat.
Before I start: having a priority queue handy makes this a lot easier to reason about and Foundation doesn’t have one built in so I put together a really basic one on top of NSMutableArray. It just makes sure to insert things in sorted order, no big deal.
I’m using Amit’s Python implementation of A* as my reference. My code looks like this:
- (NSArray *)findPathToNode:(JLFGKGraphNode *)goalNode
{
JLFGKSimplePriorityQueue *frontier = [[JLFGKSimplePriorityQueue alloc] init];
NSMapTable *cameFrom = [NSMapTable mapTableWithKeyOptions:NSMapTableObjectPointerPersonality
valueOptions:NSMapTableWeakMemory];
NSMapTable *costSoFar = [NSMapTable mapTableWithKeyOptions:NSMapTableObjectPointerPersonality
valueOptions:NSMapTableStrongMemory];
[frontier insertObject:self withPriority:0.0f];
[costSoFar setObject:[NSNumber numberWithFloat:0.0f] forKey:self];
while (frontier.count > 0) {
JLFGKGraphNode *current = [frontier get];
if (current == goalNode) {
// Done. Walk back through the cameFrom map to build up the node list, reverse and return it.
NSMutableArray *reversedPath = [NSMutableArray array];
[reversedPath addObject:current];
JLFGKGraphNode *previousNode = [cameFrom objectForKey:current];
while (previousNode != nil) {
[reversedPath addObject:previousNode];
previousNode = [cameFrom objectForKey:previousNode];
}
NSEnumerator *enumerator = [reversedPath reverseObjectEnumerator];
return [enumerator allObjects];
}
for (JLFGKGraphNode *next in current.connectedNodes) {
float newCost = [[costSoFar objectForKey:current] floatValue] + [current costToNode:next];
NSNumber *existingCost = [costSoFar objectForKey:next];
if (existingCost == nil || newCost < [existingCost floatValue]) {
[costSoFar setObject:[NSNumber numberWithFloat:newCost] forKey:next];
float priority = newCost + [next estimatedCostToNode:goalNode];
[frontier insertObject:next withPriority:priority];
[cameFrom setObject:current forKey:next];
}
}
}
// If we end up here, that means the goal node wasn't reachable from the start node.
return nil;
}That’s it. It’s a pretty straightforward algorithm. Now I’m going to go crazy overboard on the demo, because why not?
The demo for this part is in the Github repository in the directory named PathfindingDemo1. Check out GameScene.m: I manually set up a bunch of pathfinding nodes on that map (look at GameScene.sks in Xcode for them all: there are both empty nodes and sprite ones) and have a character navigate between them.
It occurs to me now that I really should have had a less linear layout, but it’s getting late and I want to wrap this up.
The graphics used in that demo come from Oryx Design Lab’s Lo-fi Fantasy Sprite Set.
The code for all of this is up on Github as JLFGamplayKit, and the repo for this post in particular is tagged as part3-pathfinding.